Online Practice Test 2a for MATH 141.

This online test was created by Brent M. Dingle. You will notice if you select the wrong answer you are notified immediately (and perhaps given a hint). Assuming everything is working (i.e. your browser supports JavaScript and has it enabled) you should have been notified of a time limit to complete this test and you should see the words: "JavaScript Enabled" immediately below.

Test Questions:

1. A class of math students can be grouped in the following sets:
A = {x | x is a woman}
B = {x | x has taken Economics}
What would be a correct way to represent the set of men who have NOT taken economics?

    {x | x Ï A AND x Ï B}
    {x | x Î A AND x Ï B}
    {x | x Ï A AND x Î B}
    {x | x Î A AND x Î B}

2. A pizza place has 15 different toppings available for pizza. How many diifferent 3 topping pizzas are possible?

    30
    45
    105
    300
    455

3. What is the x-intercept of the line passing through the point (-5, 2) with a slope of -2?

    (6, 0)
    (4, 0)
    (1/2, 0)
    (0, 1/2)
    (0, 4)

4. Four commuter trains and three express buses depart from city A to city B in the morning. Three commuter trains and three express buses operate on the return trip in the evening. In how many ways can a commuter from city A to city B complete a daily round trip via bus and/or train?

    12
    13
    21
    42
    108

5. Find the number of distinguishable permutations that can be formed from the letters in the word PHILIPPINES.

    39916800
    19958400
    6652800
    1108800
    554400

6. In how many ways can five people be seated at a round table for discussion?

    120
    25
    24
    10
    9

7. A store sold 100 computers. 80 of those sold had CD drives. 40 of those sold had cordless keyboards. How many sold did NOT have a CD drive but did have cordless keyboards?

    10
    20
    30
    40
    Not enough information given to tell.

8. How many 4 digit numbers can be formed from the numbers in the set {1,4,2,7,6,9}?     360
    480
    1240
    5400
    7800

9. Barb reaches into a bag that contains 2 red, 5 yellow, and 7 blue marbles. In how many ways can she pull out 6 marbles if exactly 4 marbles are to be the same color?

    40
    915
    1327
    43920
    132200

10. Sam needs to pick a computer password that is 5 characters long. The password must only contain numbers and letters, it must start with a letter, end in a letter, and no characters (numbers or digits) may be repeated. Moreover, his computer is case sensitive, so it distinguishes between upper and lowercase letters (i.e. 'B' is different from 'b'). How many such passwords are possible?

    23,337,600
    176,543,100
    311,875,200
    544,508,640
    572,832,000

Questions 11 to 15 are based on the following assumptions:
U = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 },
A = { all even numbers 0 to 10 },
B = { integers 0 to 10 evenly divisible by 3 },
C = { 1, 2, 3, 4, 5 }, D = { 8, 9, 10 }
(0 is an even number)

11. A Ç B = Æ

    true
    false

12. Æ Ê A

    true
    false

13. { 8, 9 } Í D

    true
    false

14. n(A È C) = ?

    2
    3
    8
    9
    12

15. 0 Î B

    true
    false

16. One card is drawn from a deck of 52 cards. In how many ways can this be done if it is to be an ace or not a club?

    40
    41
    42
    43
    44

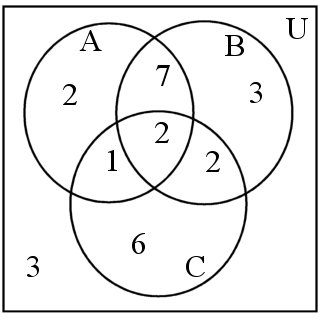
Questions 17 to 19 refer to the Venn Diagram at the right:

17. n[ (A Ç B)C Ç C ]

    2
    5
    9
    11
    23

18. n[ AC È C ]

    5
    8
    14
    17
    20

19. n[ (A Ç C) È (B Ç C) ]

    3
    5
    7
    15
    21

20. A group of 5 men and 3 women go to the movies. In how many ways can they sit in a row if Bob and Sarah *must* sit together?

    1440
    5040
    2880
    10800
    80640