Normal Distribution Table
The below tables gives values for P(Z < z) for a standard normal distribution. The first table is for non-negative z values, the second for negative z values. After the tables you will find a brief tutorial on how to actually use them to solve problems.
P(Z < z) for non-negative z values:
P(Z < z) for negative z values:
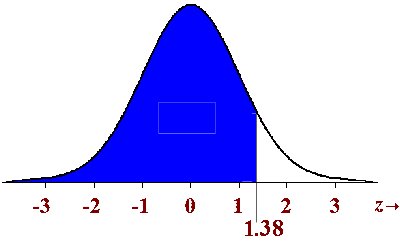
Example 1: What is P(Z < 1.38)?
So what we need to do is find the area of everything
under the normal curve "left" of where z = 1.38.
This can be illustrated like this, where we need
to find the area of the blue region:

To find the solution to this we must look it up in the above (non-negative) table. We first find 1.3 under the z heading. We then scan to the right until we are under the 0.08 heading, like so:
| z | .00 | .01 | ... | .08 | .09 |
| 0.0 | .5000 | .5040 | ... | .5319 | .5359 |
| 0.1 | .5398 | .5438 | ... | .5714 | .5753 |
| ... | ... | ... | ... | ... | ... |
| 1.2 | .8849 | .8869 | ... | .8997 | .9015 |
| 1.3 | .9032 | .9049 | ... | .9162 | .9177 |
| 1.4 | .9192 | .9207 | ... | .9306 | .9319 |
| ... | ... | ... | ... | ... | ... |
And thus we discover that P(Z < 1.38) = 0.9162.
Example 2: What is P(Z > 1.38)?
So what we need to do is find the area of everything
under the normal curve "right" of where z = 1.38.
This can be illustrated like this, where we need
to find the area of the blue region:

Notice from example 1 we know that the area of everything under
the curve to the "left" of z = 1.38 is 0.9162.
We also know that the total area under the curve is 1 (by definition).
So the area under the curve to the "right" of z = 1.38 must be:
1 - 0.9162 = 0.0838
Example 3: What is P( -0.51 < Z < 1.38)?
So what we need to do is find the area of everything
under the normal curve between Z = -0.51 and Z = 1.38.
This can be illustrated like this, where we need
to find the area of the blue region:

Recall from example 1 we know the area under the curve
"left" of z = 1.38 is 0.9162 which equals (the area of
the green region) + (the area of the blue region). So
if we can find the area of the green region we can subtract it
from 0.9162 and we will get the area of just the blue region.
Or rather: (green) + (blue) = 0.9162
So (blue) = 0.9162 - (green)
To find the green we use the table. First we look up -0.5 under
the z column and then we scan right until we are under the 0.01
heading. You should find the entry there to be 0.3050.
Thus we have:
(blue) = 0.9162 - 0.3050
(blue) = 0.6112
Thus P( -0.51 < Z < 1.38) = 0.6112.